Understanding Compressive Stress Formula in Soil Mechanics
Compressive stress is a fundamental concept in both material science and soil mechanics. It describes the stress state where a material or soil element experiences forces pushing inwards, tending to decrease its volume. In soil mechanics, understanding compressive stress is crucial for analyzing the stability of foundations, embankments, and slopes. This article will explore the compressive stress formula in soil mechanics, its derivation, application, and limitations, providing practical examples and insights for engineering students, practicing engineers, and researchers.
Defining Compressive Stress
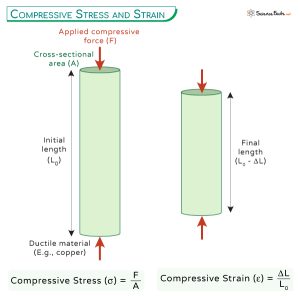
Compressive stress (often denoted as σc) is defined as the force acting perpendicularly on a surface, divided by the area over which the force is distributed. Unlike tensile stress, which pulls a material apart, compressive stress pushes the material together. It is a normal stress, meaning it acts perpendicular to the surface area under consideration.
The compressive stress formula is:
σc = F / A
Where: σc is the compressive stress (typically measured in Pascals (Pa) or pounds per square inch (psi)).
F is the compressive force acting on the surface (typically measured in Newtons (N) or pounds (lb)).
A is the area of the surface over which the force is distributed (typically measured in square meters (m2) or square inches (in2)).
In soil mechanics, the "area"Aneeds careful consideration. It represents the effective area supporting the applied load. For a foundation resting on soil,Ais the contact area between the foundation and the soil. For a soil sample in a laboratory test (e.g., a triaxial compression test),Ais the cross-sectional area of the soil specimen.
Derivation of the Compressive Stress Formula in Soil Mechanics
The compressive stress formula stems directly from the definition of stress as force per unit area. Consider a soil column supporting a structure. The weight of the structure exerts a downward force (F) on the top of the soil column. This force is distributed over the area (A) of the soil column's top surface. The soil particles resist this force, creating an internal stress within the soil. The compressive stress at any point within the soil column is then simply the force divided by the area at that point, assuming the force is uniformly distributed.
While the basic formula is straightforward, applying it in soil mechanics requires understanding the complexities of soil behavior. Soil is a multi-phase material (solid particles, water, and air) with varying properties depending on its composition, density, and stress history. Therefore, theeffective stressprinciple is frequently invoked.
The effective stress principle (Terzaghi's principle) states that the effective stress (σ') within a soil mass is the total stress (σ) minus the pore water pressure (u):
σ' = σ - u
Where: σ' is the effective stress σ is the total stress (equal to F/A in the simplest case of uniaxial compression)
u is the pore water pressure
Effective stress, not total stress, governs the soil's strength and deformation behavior. Therefore, when analyzing soil stability or settlement, it's crucial to consider the pore water pressure within the soil. Changes in pore water pressure can significantly alter the effective stress and, consequently, the soil's response to applied loads.
Applying the Compressive Stress Formula: Practical Examples
Example 1: Foundation Bearing Capacity
A rectangular foundation (2m x 3m) supports a building load of 1200 k N. Calculate the compressive stress exerted on the soil beneath the foundation.
Solution
1.Calculate the area: A = 2m 3m = 6 m2
2.Calculate the compressive stress: σc = F / A = 1200 k N / 6 m2 = 200 k Pa
Therefore, the compressive stress exerted on the soil beneath the foundation is 200 k Pa. This value would then be compared against the soil's allowable bearing capacity to determine if the foundation is adequately sized. It's crucial to remember that this is total stress. To assess stability, the effective stress should be calculated, accounting for the pore water pressure.
Example 2: Triaxial Compression Test
A cylindrical soil specimen (50mm diameter, 100mm height) is subjected to a compressive force of 5 k N in a triaxial compression test. Calculate the compressive stress on the specimen.
Solution
1.Calculate the area: A = π (d/2)2 = π (0.05m/2)2 =
0.0019635 m2
2.Calculate the compressive stress: σc = F / A = 5 k N /
0.0019635 m2 =
2546.47 k Pa ≈
2.55 MPa
Therefore, the compressive stress on the soil specimen is approximately 2.55 MPa. In a triaxial test, this compressive stress is related to thedeviator stress, which is the difference between the major principal stress and the minor principal stress. This value is crucial for determining the shear strength parameters of the soil (cohesion and angle of internal friction).
Factors Influencing Compressive Stress in Soil
Several factors influence the compressive stress distribution and magnitude within a soil mass: Applied Load: The magnitude and distribution of the applied load directly affect the compressive stress. Heavier loads result in higher stresses. Concentrated loads create stress concentrations. Soil Type: Different soil types have varying stiffness and compressibility. Stiffer soils (e.g., dense sands and gravels) experience lower compressive stresses compared to more compressible soils (e.g., soft clays) under the same load. Soil Density: Denser soils generally have higher strength and lower compressibility, leading to lower compressive strains for a given stress. Water Content and Drainage: Pore water pressure significantly affects the effective stress. Poorly drained soils can experience increased pore water pressure under load, reducing the effective stress and potentially leading to instability. Soil Structure:The arrangement of soil particles (soil structure) also influences stress distribution. A flocculated clay structure, for instance, may exhibit different stress-strain behavior compared to a dispersed clay structure.
Limitations of the Simple Compressive Stress Formula
While the formula σc = F/A is a fundamental starting point, it has limitations, especially in complex soil mechanics problems: Uniform Stress Distribution: The formula assumes a uniform stress distribution over the area A. This is often not the case, especially near the edges of loaded areas or in heterogeneous soil conditions. Finite element analysis (FEA) is often used to model more realistic stress distributions. Isotropic Material Behavior: The formula implicitly assumes that the soil is isotropic (having the same properties in all directions). Soil is typically anisotropic, particularly layered soils. Elastic Material Behavior: The simple formula does not account for the non-linear and plastic behavior of soil. Soil exhibits significant plastic deformation under load, which is not captured by a simple linear stress-strain relationship. Time-Dependent Effects: Consolidation, creep, and other time-dependent phenomena are not considered in the basic formula. These effects can significantly influence long-term settlement and stability.
To address these limitations, more advanced constitutive models are employed in soil mechanics. These models account for non-linearity, anisotropy, plasticity, and time-dependent effects. Examples include the Mohr-Coulomb model (a simple elasto-plastic model), the Cam-clay model (which accounts for volumetric hardening), and various viscoplastic models.
People Also Ask
How does the angle of repose relate to compressive stress in soil?
The angle of repose is the steepest angle at which a pile of granular material will remain stable. While not directly a compressive stress calculation, it's closely related. A higher angle of repose indicates greater shear strength. This shear strength is related to the effective stresses acting within the soil mass, which include the compressive stresses resulting from the weight of the material itself. Higher compressive stress, combined with frictional characteristics, can contribute to a larger angle of repose before the soil mass becomes unstable and fails in shear. Factors increasing shear strength (and thus the angle of repose) can be understood in terms of the effective stresses acting within the soil.
What is the difference between total stress, effective stress, and neutral stress in soil mechanics?
Total Stress (σ): The total stress is the total force per unit area acting on a soil mass. It includes the weight of the soil solids, water, and any external loads. It's what the simple F/A formula calculates.
Effective Stress (σ'): The effective stress is the stress carried by the soil skeleton (the solid particles). It's the total stress minus the pore water pressure (σ' = σ - u). Effective stress governs the soil's strength and deformation behavior.
Neutral Stress (u): The neutral stress is the pore water pressure within the soil. It does not directly contribute to the soil's strength but affects the effective stress.
The effective stress principle is crucial because only the forces transmitted through the soil skeleton are effective in resisting deformation and failure.
When are FEM (Finite Element Method) models necessary for compressive stress analysis in soil?
FEM models become necessary when: Complex Geometries: The geometry of the problem is irregular or complex, such as in the case of retaining walls, tunnels, or dams. The simple F/A formula cannot account for these geometries. Non-Homogeneous Soil Conditions: The soil profile consists of multiple layers with different properties, or there are localized zones of weak soil. Complex Loading Conditions: The loading is non-uniform or dynamic, such as in the case of earthquake loading or traffic vibrations. Non-Linear Material Behavior: The soil exhibits significant non-linear behavior, plasticity, or time-dependent effects. Coupled Analysis: The problem involves coupled phenomena, such as seepage flow and stress deformation. For instance, analyzing the consolidation of a clay layer under load requires a coupled analysis. High Accuracy Requirements: The analysis requires a high degree of accuracy, such as in the design of critical infrastructure.
FEM allows for more realistic modeling of the soil's behavior, accounting for complexities that the simple compressive stress formula cannot address.
Conclusion
Understanding compressive stress and its calculation is essential for a wide range of applications in soil mechanics. While the basic formula (σc = F/A) provides a fundamental understanding, engineers must be aware of its limitations and the importance of considering effective stress, soil properties, and other factors that influence stress distribution. For complex problems, numerical methods like FEM are indispensable tools for accurate stress analysis and reliable geotechnical design. By combining a solid understanding of the fundamental principles with advanced analytical techniques, engineers can ensure the stability and performance of structures interacting with soil.
