Commonly Used Formulas for Stress in Engineering Exams
Stress analysis is a cornerstone of mechanical engineering, materials science, and structural engineering. Whether you're designing a bridge, analyzing a pressure vessel, or assessing the reliability of a rotating component, understanding stress distribution is crucial. This article provides a comprehensive guide to the most commonly used stress formulas encountered in engineering exams and real-world applications. We will cover axial stress, shear stress, bending stress, torsional stress, principal stresses, and stress concentrations, along with practical examples and common pitfalls.
Understanding Stress: A Fundamental Concept
Stress is defined as the internal resistance offered by a material to deformation caused by external forces. It is a measure of these internal forces acting over a cross-sectional area of the material. Mathematically, stress (σ) is defined as force (F) divided by area (A):
σ = F/A
Where: σ = Stress (typically in Pascals (Pa) or pounds per square inch (psi))
F = Force (typically in Newtons (N) or pounds (lb))
A = Area (typically in square meters (m²) or square inches (in²))
It's crucial to understand thetypeof stress, as the direction and nature of the applied force greatly influence the internal stresses.
Axial Stress: Tension and Compression
Axial stress occurs when a force is applied perpendicular to the cross-sectional area of a component. It can be tensile (pulling force) or compressive (pushing force).
Formula
σ = F/A
Where: σ = Axial Stress
F = Axial Force
A = Cross-sectional area perpendicular to the force
Example
A steel rod with a diameter of 20 mm is subjected to a tensile force of 50 k N. Calculate the axial stress.
Area (A) = π (d/2)² = π (0.02 m / 2)² =
3.1416 x 10⁻⁴ m²
Stress (σ) = F/A = (50,000 N) / (3.1416 x 10⁻⁴ m²) =
159.15 MPa
Common Pitfalls
Sign Convention: Tensile stress is typically considered positive, while compressive stress is negative. Always be mindful of the sign convention in your calculations. Units: Ensure consistent units throughout the calculation. Converting everything to SI units (meters, Newtons, Pascals) is generally recommended.Area Calculation:Double-check the area calculation, especially for non-circular cross-sections.
Shear Stress: Tangential Force
Shear stress (τ) occurs when a force is applied parallel or tangential to the surface area of a component, causing it to deform by sliding or shearing.
Formula
τ = F/A
Where: τ = Shear Stress
F = Shear Force
A = Area parallel to the force
Example
A bolt with a diameter of 10 mm is used to fasten two plates together. If a shear force of 10 k N is applied to the connection, what is the shear stress in the bolt?
Area (A) = π (d/2)² = π (0.01 m / 2)² =
7.854 x 10⁻⁵ m²
Shear Stress (τ) = F/A = (10,000 N) / (7.854 x 10⁻⁵ m²) =
127.3 MPa
Important Note: Double Shear: If the bolt is subjected to shear on two planes (double shear), the area is doubled. So, A = 2 π (d/2)².
Applications: Riveted joints, bolted connections, and keyed shafts are common examples where shear stress is critical.
Bending Stress in Beams
Beams are structural elements designed to resist bending loads. Bending stress (σb) varies across the cross-section of the beam, being maximum at the outermost fibers (farthest from the neutral axis) and zero at the neutral axis.
Formula
σb = My / I
Where: σb = Bending stress
M = Bending moment at the section of interest
y = Distance from the neutral axis to the point where stress is being calculated
I = Area moment of inertia of the cross-section about the neutral axis
Maximum Bending Stress
The maximum bending stress occurs at the largest value ofy, often denoted asc*:
σmax = Mc / I
The section modulus (S) is defined as I/c, so:
σmax = M / S
Example
A cantilever beam of length 2m is subjected to a point load of 5 k N at its free end. The beam has a rectangular cross-section with a width of 50 mm and a height of 100 mm. Calculate the maximum bending stress.
Bending moment (M) at the fixed end = F L = 5000 N 2 m = 10,000 Nm
Area moment of inertia (I) = (bh³) / 12 = (0.05 m (0.1 m)³) / 12 =
4.167 x 10⁻⁶ m⁴
Distance from neutral axis to outer fiber (c) = h/2 = 0.1 m / 2 =
0.05 m
Maximum bending stress (σmax) = Mc / I = (10,000 Nm 0.05 m) / (4.167 x 10⁻⁶ m⁴) =
119.99 MPa ≈ 120 MPa
Key Concepts
Neutral Axis: The axis within the beam's cross-section where bending stress is zero. Area Moment of Inertia (I): A measure of a cross-section's resistance to bending. It depends on the shape of the cross-section. Common formulas: Rectangle (bh³/12), Circle (πd⁴/64).Section Modulus (S):A geometric property of a cross-section that relates bending moment to bending stress.
Torsional Shear Stress
Torsion occurs when a twisting moment (torque) is applied to a component, resulting in shear stress. This is common in shafts transmitting power.
Formula
τ = Tr / J
Where: τ = Torsional shear stress
T = Applied torque
r = Distance from the center of the shaft to the point where stress is being calculated
J = Polar moment of inertia of the cross-section
Maximum Torsional Shear Stress
The maximum torsional shear stress occurs at the outer surface of the shaft (r = c, where c is the radius).
τmax = Tc / J
Polar Moment of Inertia (J)
Solid Circular Shaft: J = πd⁴/32
Hollow Circular Shaft: J = π(D⁴ - d⁴)/32 (where D is the outer diameter and d is the inner diameter)
Example
A solid steel shaft with a diameter of 50 mm is subjected to a torque of 1 k N-m. Calculate the maximum torsional shear stress.
Torque (T) = 1000 Nm
Radius (c) = d/2 = 0.05 m / 2 =
0.025 m
Polar moment of inertia (J) = πd⁴/32 = π (0.05 m)⁴ / 32 =
6.136 x 10⁻⁷ m⁴
Maximum torsional shear stress (τmax) = Tc / J = (1000 Nm 0.025 m) / (6.136 x 10⁻⁷ m⁴) =
40.75 MPa
Applications: Drive shafts in vehicles, axles in rotating machinery, and torsion bars in suspension systems.
Principal Stresses and Maximum Shear Stress
Most engineering components experience complex stress states, involving combinations of normal and shear stresses. Principal stresses (σ₁ and σ₂) represent the maximum and minimum normal stresses at a point, acting on planes where the shear stress is zero.
Formulas (2D Stress State)
σ₁ = (σx + σy)/2 + √[((σx - σy)/2)² + τxy²]
σ₂ = (σx + σy)/2 - √[((σx - σy)/2)² + τxy²]
Where: σx = Normal stress in the x-direction σy = Normal stress in the y-direction τxy = Shear stress in the xy-plane
Maximum Shear Stress (τmax)
τmax = (σ₁ - σ₂)/2 = √[((σx - σy)/2)² + τxy²]
Applications: Analyzing stresses in pressure vessels, combined bending and torsion in shafts, and determining the failure criteria of materials.
How to Determine the Orientation of the Principal Planes (θp)
tan(2θp) = 2τxy / (σx - σy)
Example
At a point in a machine component, the stresses are: σx = 80 MPa, σy = -40 MPa, and τxy = 20 MPa. Determine the principal stresses and the maximum shear stress.
σ₁ = (80 - 40)/2 + √[((80 + 40)/2)² + 20²] = 20 + √(3600 + 400) = 20 + √4000 = 20 + 63.25 =
83.25 MPa σ₂ = (80 - 40)/2 - √[((80 + 40)/2)² + 20²] = 20 - √(3600 + 400) = 20 - √4000 = 20 -
63.25 = -43.25 MPa τmax = (σ₁ - σ₂)/2 = (83.25 - (-43.25))/2 =
126.5/2 =
63.25 MPa
When to Apply Principal Stress Formulas: When dealing with combined loading scenarios where multiple stress components are present. Understanding principal stresses is crucial for predicting failure, as materials typically fail along the planes of maximum shear stress or maximum tensile stress.
Stress Concentrations
Stress concentrations occur at points of geometric discontinuity, such as holes, fillets, notches, or sharp corners. The stress at these points can be significantly higher than the nominal stress in the component.
Stress Concentration Factor (Kt)
Kt = σmax / σnom
Where:
Kt = Theoretical stress concentration factor (obtained from charts or handbooks based on geometry) σmax = Maximum stress at the stress concentration σnom = Nominal stress (stress calculated without considering the stress concentration)
Formula for Maximum Stress at a Stress Concentration
σmax = Kt σnom
Example
A flat plate with a central hole is subjected to a tensile stress. The nominal stress is 50 MPa, and the stress concentration factor (Kt) at the hole is 2.5. Calculate the maximum stress at the edge of the hole.
σmax = Kt σnom = 2.5 50 MPa = 125 MPa
Mitigation Strategies
Fillets: Adding fillets (rounded corners) to sharp corners reduces stress concentrations. Hole Placement: Positioning holes away from high-stress areas minimizes their impact.Material Selection:Using materials with higher ductility can help redistribute stress.
How do you calculate hoop stress in thin-walled cylinders?
Hoop stress (σh), also known as circumferential stress, arises in thin-walled cylinders due to internal pressure. The formula is:
σh = (pr) / t
Where: σh = Hoop stress
p = Internal pressure
r = Radius of the cylinder
t = Wall thickness of the cylinder
This formula is valid when the wall thickness (t) is significantly smaller than the radius (r), typically when r/t > 10.
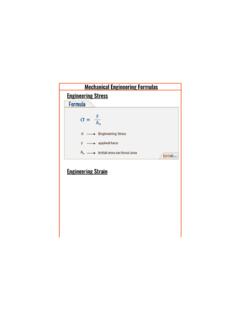
What is the difference between true stress and engineering stress?
Engineering stress is calculated using the original cross-sectional area of the material, while true stress is calculated using the instantaneous cross-sectional area during deformation. Engineering stress provides a simpler calculation but can be inaccurate at large strains, particularly during necking. True stress provides a more accurate representation of the stress experienced by the material during deformation.
Engineering stress: σ = F/A0 (A0 is original area)
True stress: σtrue = F/Ai (Ai is instantaneous area)
When should principal stress formulas be applied in design?
Principal stress formulas should be applied in design when a component is subjected to a complex stress state involving multiple stress components (normal and shear). This is common in scenarios like combined bending and torsion, pressure vessels, and situations where stress concentrations are present. Determining the principal stresses and maximum shear stress helps engineers understand the maximum stresses the material will experience and choose appropriate materials and design factors to prevent failure. Knowing the orientation of principal stresses is also crucial.
Understanding and applying these stress formulas is essential for success in engineering exams and for designing safe and reliable engineering structures and components. Remember to pay attention to units, sign conventions, and the limitations of each formula to avoid common pitfalls.
