Understanding and calculating stress is fundamental to the design and analysis of mechanical components and structures. Stress, defined as force per unit area, dictates how materials respond under load, influencing their deformation, yielding, and eventual failure. This article presents essential formulas for calculating stress encountered in various mechanical engineering applications, acting as a quick reference for students, engineers, and researchers alike.
Normal Stress Formulas
Normal stress (often denoted as σ) arises when a force acts perpendicular to a surface. This can be either tensile (pulling) or compressive (pushing).
Axial Stress
Axial stress occurs in members subjected to a force along their longitudinal axis. A common example is a rod or column under tension or compression. The formula is:
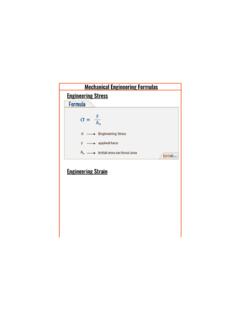
σ = F/A
Where: σ is the normal stress (usually in Pascals (Pa) or pounds per square inch (psi))
F is the applied axial force (in Newtons (N) or pounds (lb))
A is the cross-sectional area of the member (in square meters (m²) or square inches (in²))
Example
Consider a steel rod with a diameter of 20 mm subjected to a tensile force of 50,000 N. Calculate the axial stress.
- Calculate the cross-sectional area: A = πr² = π(0.01 m)² ≈
0.000314 m²
- Apply the formula: σ = F/A = 50,000 N /
0.000314 m² ≈
159.2 MPa
Therefore, the axial stress in the steel rod is approximately 159.2 MPa.
Bending Stress
Bending stress develops in beams or structures subjected to bending moments. These moments cause tensile stress on one side of the neutral axis and compressive stress on the other. The bending stress formula is:
σ = My/I
Where: σ is the bending stress
M is the bending moment at the section of interest
y is the distance from the neutral axis to the point where stress is being calculated
I is the area moment of inertia of the cross-section about the neutral axis
Example
A rectangular beam has a width (b) of 50 mm and a height (h) of 100 mm. It is subjected to a bending moment of 200 Nm. Calculate the maximum bending stress.
- Calculate the area moment of inertia: I = (bh³)/12 = (0.05 m (0.1 m)³)/12 ≈
4.17 x 10⁻⁶ m⁴
- Determine the maximum distance from the neutral axis: y = h/2 =
0.1 m / 2 =
0.05 m
- Apply the formula: σ = My/I = (200 Nm
0.05 m) / (4.17 x 10⁻⁶ m⁴) ≈
2.4 MPa
The maximum bending stress in the beam is approximately 2.4 MPa.
People Also Ask:
##### What is the difference between axial stress and bending stress?
Axial stress is caused by a force acting directly along the longitudinal axis of a member, resulting in either uniform tension or compression across the cross-section. Bending stress, however, arises from bending moments, causing a non-uniform stress distribution, with tensile stress on one side of the neutral axis and compressive stress on the other.
Shear Stress Formulas
Shear stress (often denoted as τ) arises when a force acts parallel to a surface, causing one part of the material to slide relative to the adjacent part.
Direct Shear Stress
Direct shear stress occurs when a force is applied parallel to the area resisting it. A common example is a bolt connecting two plates. The formula is:
τ = F/A
Where: τ is the shear stress
F is the applied shear force
A is the area resisting the shear force
Example
Two steel plates are joined by a bolt with a diameter of 10 mm. If the joint is subjected to a shear force of 10,000 N, calculate the shear stress in the bolt.
- Calculate the shear area: A = πr² = π(0.005 m)² ≈
0.0000785 m²
- Apply the formula: τ = F/A = 10,000 N /
0.0000785 m² ≈
127.4 MPa
Therefore, the shear stress in the bolt is approximately 127.4 MPa.
Torsional Shear Stress
Torsional shear stress develops in shafts or members subjected to a torque (twisting moment). The stress varies linearly from zero at the center to a maximum at the outer surface. The formula is:
τ = Tr/J
Where: τ is the torsional shear stress
T is the applied torque
r is the distance from the center of the shaft to the point where stress is being calculated
J is the polar moment of inertia of the cross-section
For a solid circular shaft, J = (πd⁴)/32, where d is the diameter. For a hollow circular shaft, J = (π/32)(do⁴ - di⁴), where do is the outer diameter and di is the inner diameter.
Example
A solid steel shaft with a diameter of 50 mm is subjected to a torque of 500 Nm. Calculate the maximum shear stress.
- Calculate the polar moment of inertia: J = (πd⁴)/32 = (π(0.05 m)⁴)/32 ≈
6.14 x 10⁻⁷ m⁴
- Determine the maximum radius: r = d/2 =
0.05 m / 2 =
0.025 m
- Apply the formula: τ = Tr/J = (500 Nm
0.025 m) / (6.14 x 10⁻⁷ m⁴) ≈
20.4 MPa
The maximum torsional shear stress in the shaft is approximately 20.4 MPa.
People Also Ask:
##### How do you calculate shear stress in rivets and bolts?
Shear stress in rivets and bolts is calculated using the direct shear stress formula: τ = F/A, where F is the shear force acting on the fastener and A is the cross-sectional area of the fastener resisting the shear. For single shear connections, A is simply the cross-sectional area of the rivet or bolt. For double shear connections, the shear force is distributed across two areas, so A represents twice the cross-sectional area of the rivet or bolt.
Stress Due to Pressure
Pressure vessels, such as tanks and pipes, experience stresses due to the internal pressure they contain. These stresses are critical for safe design.
Hoop Stress (Circumferential Stress) in Thin-Walled Cylinders
Hoop stress (σh) acts in the circumferential direction and resists the bursting force caused by the internal pressure. For thin-walled cylinders (where the wall thickness is less than 1/10 of the diameter), the formula is:
σh = (Pr)/t
Where: σh is the hoop stress
P is the internal pressure
r is the inside radius of the cylinder
t is the wall thickness
Longitudinal Stress in Thin-Walled Cylinders
Longitudinal stress (σl) acts along the length of the cylinder. The formula is:
σl = (Pr)/(2t)
Note that the longitudinal stress is half the hoop stress.
Example
A thin-walled cylindrical pressure vessel has an inside diameter of 1 meter and a wall thickness of 10 mm. It is subjected to an internal pressure of 2 MPa. Calculate the hoop stress and longitudinal stress.
- Calculate the radius: r = d/2 = 1 m / 2 =
0.5 m
- Calculate the hoop stress: σh = (Pr)/t = (2 MPa
0.5 m) /
0.01 m = 100 MPa
- Calculate the longitudinal stress: σl = (Pr)/(2t) = (2 MPa
0.5 m) / (2
0.01 m) = 50 MPa
The hoop stress is 100 MPa, and the longitudinal stress is 50 MPa.
Principal Stresses and Maximum Shear Stress
In many real-world scenarios, a material is subjected to a combination of normal and shear stresses. To determine the maximum stresses experienced by the material, we need to calculate the principal stresses and maximum shear stress.
Principal Stresses
Principal stresses (σ1 and σ2) are the maximum and minimum normal stresses at a point. They occur on planes where the shear stress is zero. The formulas are:
σ1,2 = (σx + σy)/2 ± √[((σx - σy)/2)² + τxy²]
Where: σx is the normal stress in the x-direction σy is the normal stress in the y-direction τxy is the shear stress in the xy-plane
Maximum Shear Stress
The maximum shear stress (τmax) is the maximum shear stress at a point. The formula is:
τmax = √[((σx - σy)/2)² + τxy²] = (σ1 - σ2)/2
Example
At a point in a stressed material, the normal stresses are σx = 80 MPa and σy = 20 MPa, and the shear stress is τxy = 30 MPa. Calculate the principal stresses and maximum shear stress.
- Calculate the principal stresses:
σ1,2 = (80 + 20)/2 ± √[((80 - 20)/2)² + 30²] = 50 ± √(30² + 30²) = 50 ± 42.43 MPa
σ1 = 50 + 42.43 =
92.43 MPa
σ2 = 50 - 42.43 =
7.57 MPa
- Calculate the maximum shear stress:
τmax = (92.43 -
7.57)/2 =
42.43 MPa
The principal stresses are approximately 92.43 MPa and
7.57 MPa, and the maximum shear stress is approximately
42.43 MPa.
People Also Ask:
##### When should principal stress formulas be applied in design?
Principal stress formulas are applied in design when a component experiences a combination of normal and shear stresses, necessitating the determination of the maximum stresses the material is subjected to. This is crucial for predicting yielding or failure under complex loading conditions. They are essential in finite element analysis (FEA) and are fundamental for applying failure theories like the maximum shear stress theory or the von Mises criterion.
Thermal Stress
Thermal stress arises when a material is subjected to a change in temperature and is constrained from expanding or contracting freely. The formula is:
σ = EαΔT
Where: σ is the thermal stress
E is the modulus of elasticity of the material α is the coefficient of thermal expansion ΔT is the change in temperature
Example
A steel bar is fixed at both ends. The temperature increases by 50°C. The modulus of elasticity of steel is 200 GPa, and the coefficient of thermal expansion is 12 x 10⁻⁶ /°C. Calculate the thermal stress.
- Apply the formula: σ = EαΔT = (200 x 10⁹ Pa) (12 x 10⁻⁶ /°C) (50 °C) = 120 MPa
The thermal stress in the steel bar is 120 MPa.
Stress Concentration
Stress concentrations occur at geometric discontinuities, such as holes, fillets, and corners, where the stress is significantly higher than the nominal stress. The stress concentration factor (Kt) is defined as the ratio of the maximum stress to the nominal stress.
σmax = Ktσnom
Determining the exact value of Kt often requires using charts, tables, or finite element analysis (FEA), as it depends heavily on the geometry of the discontinuity.
Common Pitfalls and Misconceptions
Confusing Stress and Force: Stress is forceper unit area, not just force. Understanding this distinction is crucial. Ignoring Stress Concentrations: Overlooking stress concentrations can lead to premature failure, especially in components subjected to fatigue loading. Applying Thin-Walled Formulas to Thick-Walled Vessels: The thin-walled pressure vessel formulas are only valid when the wall thickness is relatively small compared to the radius. For thick-walled vessels, more complex formulas are required. Assuming Uniform Stress Distribution:Stress is often non-uniformly distributed, particularly in bending and torsion.
Conclusion
Mastering these stress formulas and understanding their applications is essential for mechanical engineers. This article provides a starting point, but remember that real-world problems often require more advanced analysis techniques and careful consideration of material properties and loading conditions. Always double-check your calculations and consider the limitations of each formula before applying it to a design.
